
Persamaan
Kuadrat merupakan suatu persamaan polinomial berorde 2 dengan bentuk
umum dari persamaan kuadrat yaitu y=ax²+bx+c dengan a≠0 dan koefisien
kuadrat a merupakan koefisien dari x², koefisien linear b merupakan
koefisien dari x sedangkan c adalah koefisien konstan atau biasa juga
disebut suku bebas. Nilai koefisien a,b dan c ini yang menentukan
bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.
- a
menentukan seberapa cekung/cembung, jika nilai a>0 maka parabola
akan terbuka keatas. Begitu juga sebaliknya jika a<0 akan="" kebawah.="" li="" maka="" parabola="" terbuka="">

- b menentukan posisi x puncak parabola atau sumbu simetri dari kurva yang dibentuk, dengan posisi tepatnya -b/2a.

- c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau pada saat x=0.

Rumus Kuadratis
Rumus
ini biasa disebut juga dengan rumus abc, disebut demikian karena
digunakan untuk menghitung akar-kar persamaan kuadrat yang tergantung
nilai-nilai a, b dan c.

dengan pembuktian sebagai berikut.
Dari bentuk umum persamaan kuadrat,
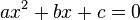
bagi kedua ruas untuk mendapatkan
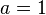
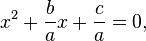
Pindahkan
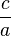
ke ruas kanan

sehingga teknik melengkapkan kuadrat bisa digunakan di ruas kiri.

Pindahkan
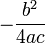
ke ruas kanan

lalu samakan penyebut di ruas kanan.
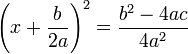
Kedua
ruas diakar (dipangkatkan setengah), sehingga tanda kuadrat di ruas
kiri hilang, dan muncul tanda plus-minus di ruas kanan.

Pindahkan
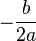
ke ruas kanan

sehingga didapat rumus kuadrat

Pada
rumus abc diatas terdapat istilah diskriminan atau determinan yaitu
notasi dalam tanda akar b²-4ac yang terkadang dinotasikan dengan huruf
D.
Persamaan kuadrat dengan koefisien-koefisien riil dapat
memiliki sebuah atau dua buah akar yang berbeda dimana akar-akarnya
dapat berupa bilangan riil atau bilangan kompleks. Terdapat 3 kemungkinan kasus :
- Diskriminan
bersifat positif, maka akan terdapat dua akar berbeda dan keduanya
riil. Untuk persamaan kuadrat yang koefisiennya berupa bilangan bulat
dan diskriminanya adalah kuadrat sempurna maka akar-akarnya adalah
bilangan rasional, atau sebaliknya dapat pula merupakan bilangan
irasional kuadrat.
- Diskriminan bernilai 0 maka akan terdapat
eksak satu akar dan riil. Hal ini terkadang disebut sebagi akar ganda,
dimana nilainya adalah

- Diskriminan
bernilai negatif maka tidak terdapat akar riil melainkan terdapat 2
buah akar kompleks yang satu sama lain merupakan konjuget kompleks.
 | dan |  |
Jadi
dapat disimpulkan akan diperoleh akar-akar berbeda jika dan hanya jika
D≠0 dan akan diperoleh akar-akar riil jika dan hanya jika D>0.
Terdapat 3 cara dalam menyelesaikan persamaan kuadrat, yaitu :
- Memfaktorkan,
untuk bentuk persamaan kuadrat ax²+bx+c=0 maka kita harus menentukan
dua buah bilangan yang jika dijumlahkan hasilnya b dan dikalikan
menghasilkan c.
- Melengkapkan kuadrat sempurna, merubah bentuk persamaan kuadrat menjadi bentuk kuadrat sempurna.
- Menggunakan rumus abc.
contoh :
1. Carilah akar-akar dari persamaan kuadrat x²-5x+6=0 !
Jawab :
x
2 – 5 x + 6 = 0 (cara memfaktorkan)
<=> ( x-2 ) ( x-3 ) = 0
<=> x- 2 = 0 atau x – 3 = 0
<=> x = 2 atau x = 3
Sehingga himpunan penyelesaiannya adalah {2, 3}
2. Tentukan himpunan penyelesaian dari persamaan x
2 + 2x – 15 = 0 !
Jawab : x
2 + 2x – 15 = 0 (cara melengkapkan kuadrat sempurna)
x
2 + 2x = 15
Agar x
2 + 2x menjadi bentuk kuadrat sempurna maka harus ditambah dengan kuadrat dari setengah koefisien (½ .2)
2 = 1
Dengan menambahkan 1 pada kedua ruas, diperoleh :
x
2 + 2x + 1 = 15 + 1
<=> (x + 1)
2 = 16
<=> x + 1 = ± √16
<=> x + 1 = ± 4
<=> x + 1 = 4 atau x + 1 = -4
<=> x = 4 – 1 atau x = -4 -1
<=> x = 3 atau x = -5
Sehingga himpunan penyelesaiannya adalah {3, -5}
3. Tentukan himpunan penyelesaian persamaan x
2 + 4x – 12 = 0 !
Penyelesaian : (menggunakan rumus abc)
Berdasarkan persamaan diketahui bahwa a =1, b = 4, c = -12 selanjutnya koefisien tersebut kita masukkan dalam rumus abc.
x
1,2 = (- b ± √b
2 – 4ac) /2a
<=> x
1,2 =( - 4 ± √42 – 4 . 1. (-12) )/2.1
<=> x
1,2 = (- 4 ± √16 + 48)/2
<=> x
1,2 = (- 4 ± √64)/2
<=> x
1,2 = (- 4 ± 8)/2
<=> x
1,2 = (- 4 + 8) /2 atau x
1,2 = (- 4 - 8 )/2
<=> x
1 = 2 atau x
2 = -6
jadi himpunan penyelesaiannya adalah {2,-6}
4. Tentukan persamaan kuadrat yang akar-akarnya 2 dan 5?
Jawab :
Cara 1 : Memakai faktor, dengan memasukkan nilai akar kedalam rumus
(x-x1) (x-x2) = 0
x
1 = 2 dan x
2 = 5
Maka (x-x
1) (x-x
2) = 0
<=> (x-2) (x-5) = 0
<=> x
2 – 7x + 10 = 0
Jadi persamaan kuadratnya x
2 – 7x + 10 = 0
Cara 2 : Memakai rumus jumlah dan hasil kali akar-akar yaitu x
2 – (x
1+x
2)x + x
1.x
2 = 0
x
1 = 2 dan x
2 = 5
Maka x
2 – (x
1+x
2)x + x
1.x
2 = 0
Dengan (x
1 + x
2) = 2 + 5 = 7
x
1. x
2 = 2.5 = 10
Jadi persamaan kuadratnya x
2 – 7x + 10 = 0
Rumus jumlah dan hasil kali akar-akar diperoleh dari penjumlahan dan perkalian rumus abc, perhatikan penjelasan berikut ini.
x
1 + x
2 =
-b + √ b2 – 4ac + – b – √ b2 – 4ac
2a 2a
= -2b/a
= -b/a
x
1 .x
2 =
-b + √ b2 – 4ac . – b – √ b2 – 4ac
2a 2a
= ( b
2 – (b
2 – 4 ac)) / 4a
2
= 4ac /4a
2
= c/a
Dari
rumus umum persamaan kuadrat y=ax²+bx+c=0, jika kita mencari akar-akar
menggunakan pemfaktoran b diperoleh dari penjumlahan akar-akar dan c
diperoleh dari perkalian akar-akar ( baca kembali metode penyelesaikan
persamaan kuadrat diatas) sehingga kita dapat memperoleh pernyataan
x2 – (x1 + x2) x + x1.x2 = 0
|
|
Sekian dulu penjelasan mengenai Persamaan Kuadrat, semoga bermanfaat dan jika sobat menemukan ada yang kurang pas, mohon koreksinya ya….. dan jangan lupa baca juga Materi Bilangan Kompleks atau Fungsi Eksponen dan Logaritma.








 dengan pembuktian sebagai berikut.
dengan pembuktian sebagai berikut.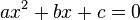
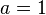
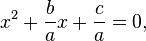
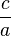 ke ruas kanan
ke ruas kanan

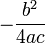 ke ruas kanan
ke ruas kanan
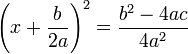

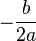 ke ruas kanan
ke ruas kanan












